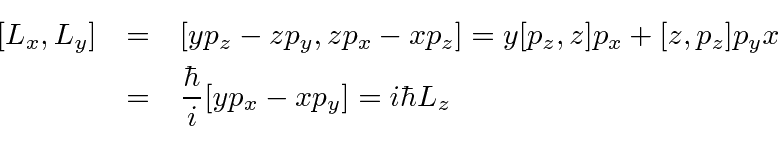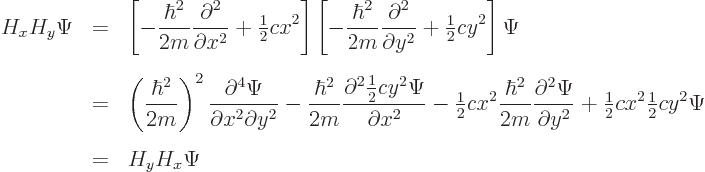Table 1 from Classical Systems and Representations of (2+1) Newton-Hooke Symmetries | Semantic Scholar

quantum mechanics - A derivation of the canonical commutation relations (CCR) written by Dirac? - Physics Stack Exchange

lecture 2 Commutation relation in quantum mechanics|Ever heard of quantum operators and commutators? - YouTube
![Tamás Görbe on X: "Commutation relations like this form the basis of quantum mechanics. This example expresses the connection between position (X) and momentum (P): [X,P]=XP-PX=ih/2π, where h is Planck's constant. It Tamás Görbe on X: "Commutation relations like this form the basis of quantum mechanics. This example expresses the connection between position (X) and momentum (P): [X,P]=XP-PX=ih/2π, where h is Planck's constant. It](https://pbs.twimg.com/media/E_o9UrsXsAQCKX1.png:large)
Tamás Görbe on X: "Commutation relations like this form the basis of quantum mechanics. This example expresses the connection between position (X) and momentum (P): [X,P]=XP-PX=ih/2π, where h is Planck's constant. It

quantum mechanics - Spatial Translation Commutation with Position Operator in QM - Physics Stack Exchange

complex analysis - Trouble Deriving the Canonical Commutation Relation from the Product Rule - Mathematics Stack Exchange
GitHub - nbeaver/commutator-table: A table of commutator relations for quantum mechanical operators in a LaTeX/CSV table.
![SOLVED: Mechanics commutation relations in quantum mechanics are given by [z, Pv] = [u, P-] = 0, [y, Pv] = ih, and [2, P:] = i. The operator J = TPv-YPz represents SOLVED: Mechanics commutation relations in quantum mechanics are given by [z, Pv] = [u, P-] = 0, [y, Pv] = ih, and [2, P:] = i. The operator J = TPv-YPz represents](https://cdn.numerade.com/ask_images/220b82a7135042d2901ee8e0911432b2.jpg)


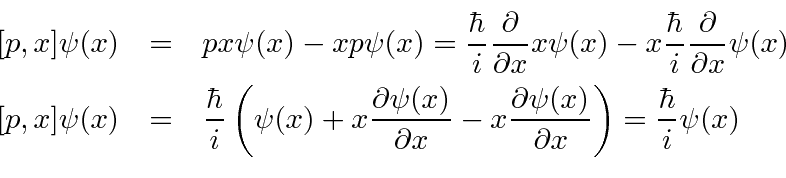






![Quantum Mechanics | Commutation of Operators [Example #2] - YouTube Quantum Mechanics | Commutation of Operators [Example #2] - YouTube](https://i.ytimg.com/vi/3XX__CV8ks8/maxresdefault.jpg)